Grafy elementárnych funkcií
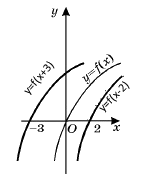
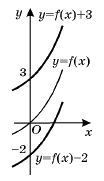
Grafy najznámejších elementárnych funkcií sú znázornené nižšie v abecednom usporiadaní. Definície uvedených funkcií spolu s kompletnou teóriou nájdete v sekcii študijné materiály, všetky dôležité vzorce a vzťahy medzi nimi v sekcii vzorce a vzťahy. V prípade, ak by Ste medzi nimi nenašli graf, ktorý potrebujete, dajte nám vedieť a v adekvátnom čase ho zaradíme. Predpis každej zloženej funkcie jednej premennej vzniká rôznymi kompozíciami elementárnych funkcií. Každá takáto kompozícia spôsobí zmenu grafu funkcie a to vo forme posunu alebo rozpínania, resp. sťahovania grafu funkcie po súradných osiach. Zmeny sú znázornené na nasledovných obrázkoch.
Cyklometrické funkcie:
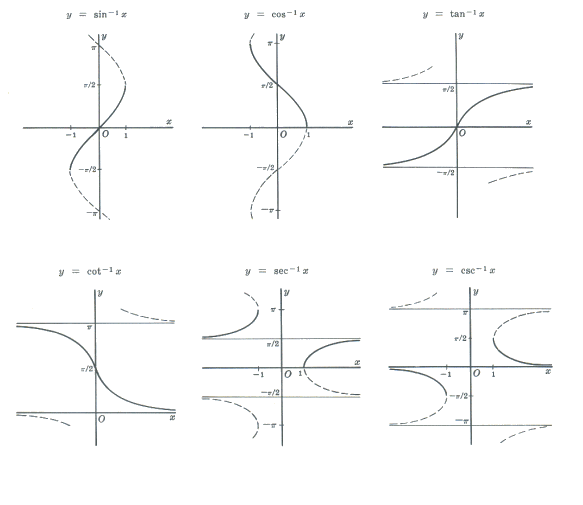
Goniometrické (trigonometrické) funkcie \(y=\sin x\), \(y=\cos x\), \(y=\hbox{tg}\, x\), \(y=\hbox{cotg}\, x\), \(y=\sec x\) a \(y=\hbox{cosec}\, x\) sú periodické, no nie prosté funkcie, a preto nemajú inverzné funkcie. Každá z nich je však na istom maximálnom intervale prostá, a preto má na ňom inverznú funkciu. Tieto inverzné funkcie sa nazývajú cyklometrické funkcie a patria tu funkcie: \(y=\arcsin x\), \(y=\arccos x\), \(y=\hbox{arctg}\, x\) a \(y=\hbox{arccotg}\, x\). Menej známe sú \(y=\sec^{-1} x\) a \(y=\hbox{cosec}^{-1} x\).
Exponenciálne funkcie:
Graf exponenciálnej funkcie \(y=a^x\) závisí od hodnoty základu \(a\gt0\).
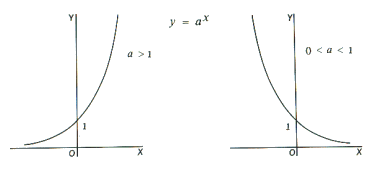
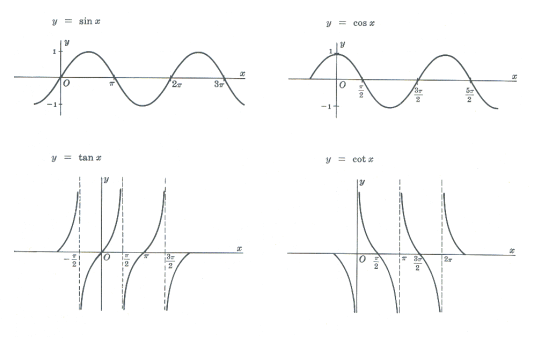
Goniometrické (trigonometrické) funkcie:
Medzi goniometrické funkcie patria funkcie: \(y=\sin x\), \(y=\cos x\), \(y=\hbox{tg}\, x\) a \(y=\hbox{cotg}\, x\). Menej známe sú \(y=\hbox{sec}\, x\) a \(y=\hbox{cosec}\, x\).
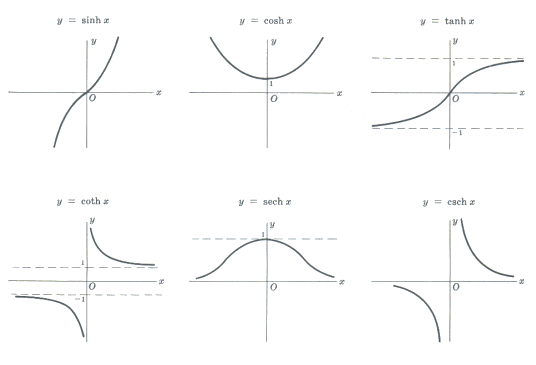
Hyperbolické funkcie:
Medzi hyperbolické funkcie patrí: \(y=\sinh x\), \(y=\cosh x\), \(y=\hbox{tgh}\, x\), \(y=\hbox{coth}\, x\), \(y=\hbox{sech}\, x\) a \(y=\hbox{csch}\, x\).
Kvadratické funkcie:
Lineárne funkcie:
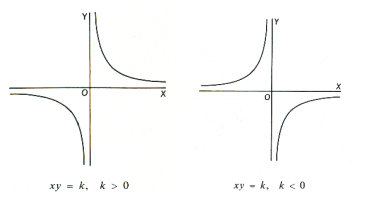
Lineárne lomené funkcie:
Graf lineárnej lomenej funkcie \(y=\frac{k}{x}\) závisí od hodnoty \(k\).
Logaritmické funkcie:
Graf logaritmickej funkcie \(y=\log_a x\) závisí od hodnoty základu \( a\gt 0\).

Mocninové funkcie:
Graf mocninovej funkcie \(y=x^n\) závisí od hodnoty exponentu \(n\). Podľa toho či je \(n\) - párne alebo \(n\) - nepárne.
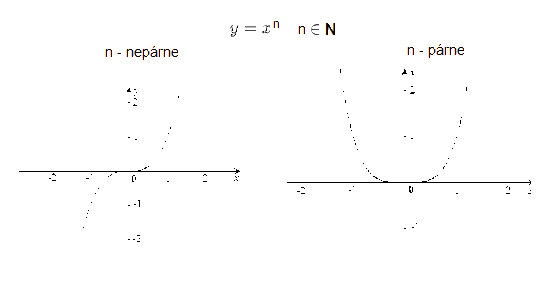
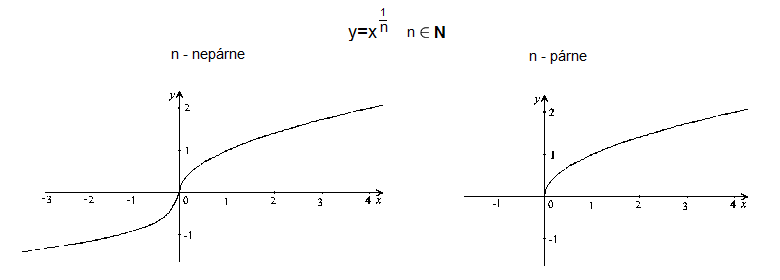
Páči sa Vám tento web venovaný matematike?
