Viacrozmerné integrály

Dvojný integrál

Nech \(f:\mathbb{R}^2\supset A\to \mathbb{R}\) je spojitá funkcia a nech \(\sigma\subset A\) je ohraničená a uzavretá oblasť. Oblasť \(\sigma\) rozdelíme na \(n\) častí \(\sigma_i\), pre \(i=1,\dots,n\) tak, aby \(\sigma=\displaystyle\bigcup_{i=1}^n\sigma_i\) a žiadne dve rôzne oblasti nemali spoločné vnútorné body. Pre každú oblasť \(\sigma_i\) dostávame:

• pre bod \(P_i\in \sigma_i\) nech \(f(P_i)\) je hodnota funkcie \(f\) v bode \(P_i\);
• nech \(\Delta \sigma_i\) prestavuje plošný obsah oblasti \(\sigma_i\);
• pre \(f\geq 0\) predstavuje výraz \(f(P_i)\Delta\sigma_i\)  objem telesa s podstavou \(\sigma_i\) a výškou \(f(P_i)\).

Objem telesa zostrojeného nad oblasťou \(\sigma\), ktoré je  ohraničené funkciou \(f\) a rovinou \(z=0\) je     \[V_n\approx \sum_{i=1}^n f(P_i)\Delta\sigma_i=S(f,D_n),\]kde \(S(f,D_n)\) je integrálny súčet pre dvojný integrál prislúchajúci deleniu \(D_n\) a danému výberu bodov \(P_i\). Nech pre \(n\in \mathbb{N}\) je \(D_n\) delenie oblasti \(\sigma\) na malé oblasti \(\sigma_i\) a nech \(d(\sigma_i)\) je priemer oblasti \(\sigma_i\). Postupnosť delení \(\{D_n\}_{n=1}^\infty\) je normálna postupnosť delení, ak \[\lim_{n\to\infty}d(\sigma_i)=0.\]Číslo \(I\) je dvojným integrálom funkcie \(f\) na oblasti \(\sigma\), ak pre každú normálnu postupnosť delení \(\{D_n\}_{n=1}^\infty\) oblasti \(\sigma\) a pre ľubovoľné výbery bodov v súčtoch \(S(f,D_n)\) je  \[\displaystyle\lim_{n\to \infty}S(f,D_n)=I.\]Ak existuje dvojný integrál funkcie \(f\) na oblasti \(\sigma\), tak funkcia je integrovateľnou na oblasti \(\sigma\) a príslušný integrál označujeme \[\displaystyle\int_{\sigma}\int f(x,y)d\sigma\; \hbox{ alebo } \;\displaystyle\int_{\sigma}\int f(x,y)dx dy.\]Ohraničená oblasť \(\sigma\) je merateľná, ak  existuje \(\displaystyle\int_{\sigma}\int dxdy\), a pre merateľnú oblasť \(\sigma\) je obsahom oblasti \(\sigma\) číslo \[m(\sigma)=\displaystyle\int_{\sigma}\int dxdy.\]

Vlastnosti a výpočet dvojného integrálu

Nech  \(f\), \(g\) sú integrovateľné funkcie na oblasti \(\sigma\) a nech \(k\in\mathbb{R}\). Potom aj funkcie \(f+g\), \(k.f\) sú integrovateľné na oblasti \(\sigma\) a platí \[ \displaystyle\int_{\sigma}\int\left[f(x,y)+g(x,y)\right]d\sigma=\int_{\sigma}\int f(x,y)d\sigma+\int_{\sigma}\int g(x,y)d\sigma,\]\[\int_{\sigma}\int k.f(x,y)d\sigma=k\int_{\sigma}\int f(x,y)d\sigma.\]

Nech funkcia \(f\) je integrovateľná na oblastiach \(\sigma_1\), \(\sigma_2\), ktoré tvoria delenie oblasti \(\sigma\). Potom je funkcia \(f\) integrovateľná aj na oblasti \(\sigma\) a platí \[ \displaystyle\int_{\sigma}\int f(x,y)d\sigma=\int_{\sigma_1}\int f(x,y)d\sigma+\int_{\sigma_2}\int f(x,y)d\sigma.\]

Závislosť integrovania od elementárnej oblasti:

Výrazom \(\sigma_{xy}\) označujeme elementárnu oblasť vzhľadom na os \(o_x\) určenú vzťahom \[\sigma_{xy}=\{[x,y]\in \mathbb{R}^2:a\leq x\leq b \wedge \alpha(x)\leq y \leq\beta(x)\},\] kde \(\alpha,\beta\in\mathcal {C}(\left\langle a,b\right\rangle)\). Výrazom \(\sigma_{yx}\) označujeme elementárnu oblasť vzhľadom na os \(o_y\) určenú vzťahom \[\sigma_{yx}=\{[x,y]\in \mathbb{R}^2:c\leq y\leq d \wedge \gamma(y)\leq x \leq\delta(y)\},\] kde \(\gamma,\delta\in\mathcal {C}(\left\langle c,d\right\rangle)\).

Nech funkcia \(f\) je integrovateľná na oblasti \(\sigma_{xy}\) a nech pre každé \(x\in \left\langle a,b\right\rangle\) existuje \(\displaystyle\int_{\alpha(x)}^{\beta(x)} f(x,y)dy\). Potom platí \[ \displaystyle\int_{\sigma_{xy}}\int f(x,y)d\sigma=\int_a^b\left(\int_{\alpha(x)}^{\beta(x)} f(x,y)dy\right) dx.\]Nech funkcia \(f\) je integrovateľná na oblasti \(\sigma_{yx}\) a nech pre každé \(y\in \left\langle c,d\right\rangle\) existuje \(\displaystyle\int_{\gamma(y)}^{\delta(y)} f(x,y)dx\). Potom platí \[ \displaystyle\int_{\sigma_{yx}}\int f(x,y)d\sigma=\int_c^d\left(\int_{\gamma(y)}^{\delta(y)} f(x,y)dx\right) dy.\]

Transformácia dvojného integrálu

Transformáciu dvojného integrálu používame vtedy, keď integračná oblasť vyjadrená v pravouhlých súradniciach nie je vhodná pre výpočet integrálu. 

Nech v rovine \(O_{xy}\) je dané zobrazenie z oblasti \(D\) ohraničenej krivkou \(L\) na odpovedajúcu oblasť \(D^{'}\) ohraničenú krivkou \(L^{'}\). Predpokladajme, že súradnice \(x\) a \(y\) sú funkcie nových premenných  \(u\) a \(v\)  v tvare \[x=x(u,v)\quad\hbox{a}\quad y=y(u,v),\quad\quad (1)\] pričom  \(x=x(u,v)\) a \(y=y(u,v)\) sú spojité funkcie, ktoré majú parciálne derivácie prvého rádu v oblasti \(D^{'}\). K zobrazeniu existuje inverzné  zobrazenie, a tak súradnice bodov oblasti  \(D^{'}\) sú funkciami premenných \(x\) a \(y\) \[u=u(x,y)\quad\hbox{a}\quad v=v(x,y).\quad\quad (2)\]Zobrazenie oblasti \(D^{'}\) na oblasť \(D\) je regulárne, ak:

• funkcie \(x=x(u,v)\), \(y=y(u,v)\) majú spojité parciálne derivácie v oblasti \(D^{'}\),
• determinant \[J(u,v)= \left|\begin{matrix}\frac{\partial x}{\partial u} & \frac{\partial y}{\partial u} \\ \frac{\partial x}{\partial v} & \frac{\partial y}{\partial v}\end{matrix}\right|\neq 0\quad\quad (J)\]pre všetky body \((u,v)\in D^{'}\).

Výraz \(J(u,v)\), definovaný predpisom vo vzťahu \((J)\), je Jacobiho funkcionálny determinant alebo Jacobián zobrazenia.

Nech funkcia \(f(x,y)\) je integrovateľná na oblasti \(D\) a nech zobrazenie dané rovnicami \((1)\) je prosté a regulárne. Potom  \[ \displaystyle\int_{D}\int f(x,y)dxdy= \displaystyle\int_{D^{'}}\int f(x(u,v),y(u,v))\left|J\right|dudv,\] kde  \(|J|\) je absolútna hodnota jacobiánu \(J(u,v)\).

Transformácia pomocou polárnych súradníc:

Nech \(P\) je pevný bod roviny. Polpriamka \(\vec{o}\) so začiatočným bodom \(P\) a otáčanie v kladnom smere okolo bodu   \(P\) v rovine určujú polárnu súradnicovú sústavu \((P,\vec{o},\varphi)\). Bod  \(P\) je začiatok súradnicovej sústavy a polpriamka \(\vec{o}\) je polárna os tejto sústavy.

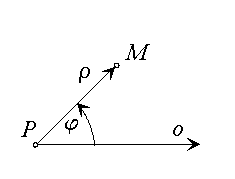
Každému bodu  \(M\) roviny je priradená dvojica reálnych čísel \((\rho,\varphi)\), kde \(\rho=|PM|\) a \(\displaystyle\varphi=|(\vec{o},\vec{PM})|\).  Usporiadaná dvojica \((\rho,\varphi)\) predstavuje polárne súradnice bodu \(M\), číslo \(\rho\) je modul a \(\varphi\) je polárny uhol. Zobrazenie medzi karteziánskou  sústavou \((O,x,y)\) a polárnou sústavou \((P,\vec{o},\varphi)\) je určené rovnicami \[x=\rho\cos \varphi,\quad \hbox{pre}\quad 0\leq\rho\leq\infty\]\[y=\rho\sin \varphi, \quad\hbox{pre}\quad 0\leq \varphi \leq 2\pi.\]Polárna transformácia je prosté a regulárne zobrazenie  na množine \[\Omega^{*}=\{[\rho,\varphi]:0\lt\rho\lt \infty,\,0\lt \varphi \lt 2\pi \}\]a pre Jacobián polárneho zobrazenia platí  \[J(\rho,\varphi)=\rho.\]