Lichobežníková metóda

Numerické integrovanie patrí k štandardným aproximačným metódam a používa sa najmä v prípadoch, ak nevieme nájsť k danej integrovanej funkcii \(f(x)\) jej primitívnu funkciu \(F(x)\), a tak je potrebné pre výpočet určitého integrálu \(\displaystyle\int_a^b f(x)dx\) rozdeliť interval \(\left<a,b\right>\) na menšie časti. Na týchto častiach (intervaloch) sa funkcia \(f(x)\) aproximuje Langrangeovým polynóm, ktorého graf je priamka spájajúca body grafu funkie \(f(x)\) v krajných bodoch jednotlivých intervalov. Keďže každá takáto oblasť nad jednotlivými intervalmi má tvar lichobežníka,  poznáme túto metódu pod názvom lichobežníková metóda.

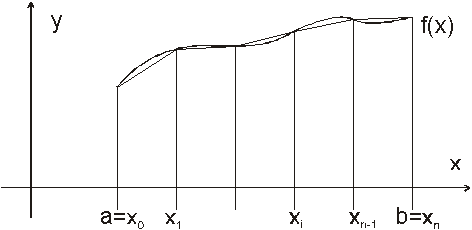
Interval integrovania  \(\left<a,b\right>\) rozdelíme na \(n\) intervalov rovnakej dĺžky  \(h=\frac{b-a}{n}\) s uzlovými bodmi \[a=x_0\lt x_1\lt x_2\lt \dots \lt x_{n-1}\lt x_n=b_n,\]kde \(x_i=x_0+ih\) pre \(i=0,1,\dots,n\).  Pre každé \(i=0,1,\dots,n-1\) budeme na intervale \[\left<a+ih,a+(i+1)h\right>=\left<x_i,x_{i+1}\right>\] funkciu \(f(x)\) aproximovať Langrangeovým interpolačným polynónom prvého stupňa, a dostávame približnú hodnotu určitého integrálu \[\int_{x_i}^{x_{i+1}}f(x)dx\approx\int_{x_i}^{x_{i+1}}L_1(x,x_i,x_{i+1})dx=\frac{h}{2}\left[f(x_i)+f(x_{i+1})\right].\]Z aditívnej vlastnosti určitého integrálu potom vyplýva \[\int_{a}^{b}f(x)dx=\int_{a}^{a+h}f(x)dx+\int_{a+h}^{a+2h}f(x)dx+\dots+\int_{a+(n-1)h}^{b}f(x)dx=\]\[=\int_{x_0}^{x_1}L_1(x,x_0,x_1)dx+\int_{x_1}^{x_2}L_1(x,x_1,x_2)dx+\dots+\int_{x_{n-1}}^{x_n}L_1(x,x_{n-1},x_n)dx+R(f)=\]\[=\frac{h}{2}\left[f(x_0)+2f(x_1)+2f(x_2)+\dots+2f(x_{n-1})+f(x_n)\right]+R(f),\]kde pre chybu \(R(f)\), ktorej sme sa dopustili, platí \[R(f)=-\frac{(b-a)^3}{12n^2}f^{\prime\prime}(\xi),\quad\xi\in\left<a,b\right>.\]Pre horný odhad chyby lichobežníkovej metódy dostávame vzťah \[\left|R(f)\right|\leq\frac{(b-a)^3}{12n^2}M_2,\quad M_2=\max_{x\in\left<a,b\right>}\left|f^{\prime\prime}(x)\right|.\]