Newtonova metóda

Newtonova metóda patrí k iteračným metódam, ktorými hľadáme numerické riešenie nelineárnych rovníc, t.j. reálne korene rovnice \(f(x)=0\), kde \(f(x)\) je spojitá reálna funkcia definovaná na nejakom intervale \((c,d)\). Koreňom rovnice \(f(x)=0\) je číslo \(\alpha\), pre ktoré \(f(\alpha)=0\). Výpočet koreňov začíname metódou separácie koreňov, t.j. určíme intervaly, v ktorých leží práve jeden koreň.

Separáciou koreňov určíme uzavretý interval \(\left<a,b\right>\), v ktorom leží jeden reálny koreň rovnice \(f(x)=0\). Predpokladajme, že funkcia \(f(x)\) je dvakrát diferencovateľná a funkcie \(f^{\prime}(x)\), \(f^{\prime\prime}(x)\) na intervale \(\left<a,b\right>\) nemenia znamienko. V nultom kroku zvolíme začiatočnú  iteráciu \(x_0\) tak, aby platilo \(f(x_0).f^{\prime\prime}(x_0)\gt 0\). Ďalšie iterácie pre \(n=0,1,2,\dots\) vypočítame podľa vzťahu \[x_{n+1}=x_n-\frac{f(x_n)}{f^{\prime}(x_n)}.\]Postupnosť takýchto iterácií bude konvergovať k presnému riešeniu \(\alpha\), ak sú splnené vyššie zmienené predpoklady pre funkciu \(f(x)\). Iteračný proces končí, ak je splnená podmienka \[f(x_{n+1}-\varepsilon).f(x_{n+1}+\varepsilon)\lt 0,\]kde \(\varepsilon\) je požadovaná presnosť výpočtu. Približná hodnota koreňa \(\alpha\) je potom rovná \(x_{n+1}\). Odhad chyby iterácie \(x_{n+1}\) vykonáme na základe vzťahu \[\left|x_{n+1}-\alpha\right|\leq\frac{|f(x_{n+1})|}{M},\]kde \(\displaystyle M=\min_{x\in\left<a,b\right>}\left|f^{\prime}(x)\right|\)  a \(\alpha\) je presná hodnota koreňa.

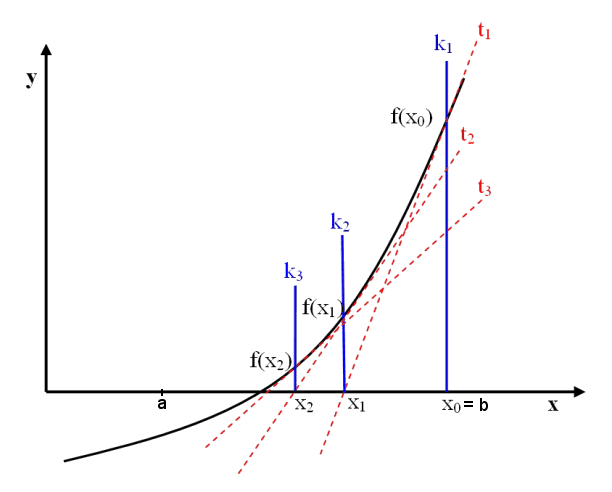
Newtonovu metódu poznáme aj pod názvom metóda dotyčníc pretože pri jednotlivých iteráciách je využitá myšlienka dotyčníc ku grafu funkcie \(f(x)\). Nech napr. iteračný proces začína v krajnom bode \(x_0=b\). Dotyčnica \(t_1\) ku grafu funkcie \(f(x)\) v dotykovom bode \(T[x_0,f(x_0)]\) pretína os \( x\) v bode \(A=[x_1,0]\). V ďalšom kroku dotyčnica \(t_2\) ku grafu funkcie \(f(x)\) v dotykovom bode \(T[x_1,f(x_1)]\) pretína os \( x\) v bode \(B=[x_2,0]\) atď.