Regresná a korelačná analýza

Regresná analýza

Hlavným cieľom regresnej analýzy je preskúmať a charakterizovať vzájomné vzťahy medzi premennými. Jej úlohou je nájsť matematickú funkciu nazývanú aj regresnú funkciu, resp. regresný model, ktorý bude čo najlepšie popisovať priebeh závislosti medzi premennými. Podľa počtu neznámych delíme regresnú analýzu na:

• jednoduchú analýzu -  ak sa zaoberáme jednou nezávislou premennou, závislá premenná \(Y\) bude závisieť od nezávislej premennej \(X\). Užitočnou pomôckou pri vyšetrovaní závislosti je grafická metóda využitím bodového grafu tvoreného bodmi \([x_i,y_i]\), pre \(i=1,\dots,n\) v rovine, kde \(x_i\) a \(y_i\) sú hodnoty skúmaných premenných \(X\) a \(Y\). Na základe priebehu bodového grafu sa následne snažíme rozhodnúť, o aký typ závislosti sa jedná: lineárny, kvadratický, hyperbolický, exponenciálny atď.
• viacnásobnú analýzu - ak uvažujeme  väčší počet nezávislých premenných.

Lineárna regresia:

Lineárny regresný model popisuje lineárnu závislosť medzi závislou premennou \(Y\) a nezávislou premennou \(X\). Môžeme ho popísať rovnicou \[Y=\beta_0+\beta_1X+\varepsilon,\] kde \(\beta_0\), \(\beta_1\) sú parametre modelu a \(\varepsilon\) je náhodná chyba pozorovania. Bodovým odhadom je lineárna funkcia \[\widehat{y}=b_0+b_1x,\] kde \(\widehat{y}\) je teoretická hodnota a \(b_0\), \(b_1\) sú bodové odhady parametrov \(\beta_0\), \(\beta_1\).

Parametre \(b_0\), \(b_1\) odhadujeme pomocou metódy najmenších štvorcov (MNŠ) z výpočtového tvaru:\[b_0.n+b_1.\sum_{i=1}^n x_i=\sum_{i=1}^ny_i,\] \[b_0.\sum_{i=1}^n x_i+b_1.\sum_{i=1}^n x_i^2=\sum_{i=1}^nx_i.y_i.\]

Získanú sústavu rovníc môžeme vyriešiť napr.  Cramerovým pravidlom a tak koeficienty \(b_0\), \(b_1\) vieme vyjadriť v tvare: \[b_1=\frac{\overline{xy}-\overline{x}.\overline{y}}{\overline{x^2}-(\overline{x})^2};\;\;\;b_0=\overline{y}-b_1.\overline{x}.\] Po následnom dosadení dostávame prvú regresnú priamku \[\widehat{Y}-\overline{y}=\frac{s_{xy}}{s_x^2}.(X-\overline{x}),\] kde \(s_{xy}=\overline{xy}-\overline{x}.\overline{y}\) a \(s^2_x=\overline{x^2}-(\overline{x})^2\).

V prípade regresného modelu \[X=\alpha_0+\alpha_1Y+\varepsilon,\] je bodovým odhadom lineárna funkcia \[\widehat{x}=a_0+a_1y,\] kde \(\widehat{x}\) je teoretická hodnota a \(a_0\), \(a_1\) sú bodové odhady parametrov \(\alpha_0\), \(\alpha_1\). Parametre \(a_0\), \(a_1\) odhadujeme analogicky pomocou metódy najmenších štvorcov (MNŠ) z výpočtového tvaru:\[a_0.n+a_1.\sum_{i=1}^n y_i=\sum_{i=1}^nx_i,\]\[a_0.\sum_{i=1}^n y_i+a_1.\sum_{i=1}^n y_i^2=\sum_{i=1}^nx_i.y_i.\] Hľadané koeficienty \(a_0\), \(a_1\) vieme vyjadriť v tvare: \[a_1=\frac{\overline{xy}-\overline{y}.\overline{x}}{\overline{y^2}-(\overline{y})^2};\;\;\;a_0=\overline{x}-a_1.\overline{y}.\] Po následnom dosadení dostávame druhú regresnú priamku  \[\widehat{X}-\overline{x}=\frac{s_{xy}}{s_y^2}.(Y-\overline{y}),\] kde \(s_{xy}=\overline{xy}-\overline{x}.\overline{y}\) a \(s^2_y=\overline{y^2}-(\overline{y})^2\).

Kvadratická regresia:

Ak je vzťah medzi  premennými \(X\) a \(Y\) kvadratický, tak  regresný model vyjadrujeme rovnicou \[Y=\beta_0+\beta_1X+\beta_2X^2+\varepsilon,\] kde \(\beta_0\), \(\beta_1\), \(\beta_2\) sú parametre modelu a \(\varepsilon\) je náhodná chyba pozorovania. Bodovým odhadom je kvadratická funkcia \[\widehat{y}=b_0+b_1x+b_2x^2,\] kde \(\widehat{y}\) je teoretická hodnota a \(b_0\), \(b_1\), \(b_2\) sú bodové odhady parametrov \(\beta_0\), \(\beta_1\) a \(\beta_2\).

Parametre \(b_0\), \(b_1\), \(b_2\) odhadujeme pomocou metódy najmenších štvorcov (MNŠ) z výpočtového tvaru:\[b_0.n+b_1.\sum_{i=1}^n x_i+b_2.\sum_{i=1}^n x_i^2=\sum_{i=1}^ny_i,\] \[b_0.\sum_{i=1}^n x_i+b_1.\sum_{i=1}^n x_i^2+b_2.\sum_{i=1}^n x_i^3=\sum_{i=1}^nx_i.y_i,\] \[b_0.\sum_{i=1}^n x_i^2+b_1.\sum_{i=1}^n x_i^3+b_2.\sum_{i=1}^n x_i^4=\sum_{i=1}^nx_i^2.y_i.\]

Regresné funkcie vhodnou transformáciou prevádzame na lineárnu regresiu:

• hyperbolická regresia - model, v ktorom je závislosť popísaná hyperbolickou funkciou \[Y=\beta_0+\frac{\beta_1}{X}+\varepsilon.\] Transformáciou \(T=\frac{1}{X}\) prevádzame bodový odhad \(\widehat{y}=b_0+\frac{b_1}{X}\) na lineárny model \[\widehat{y}=b_0+b_1T.\]
• logaritmická regresia - model, v ktorom je závislosť popísaná logaritmickou funkciou \[Y=\beta_0+\beta_1\ln X+\varepsilon.\] Transformáciou \(T=\ln {X}\) prevádzame bodový odhad \(\widehat{y}=b_0+b_1\ln {X}\)  na lineárny model \[\widehat{y}=b_0+b_1T.\]
• exponenciálna regresia - model, v ktorom je závislosť popísaná exponenciálnou funkciou \[Y=\beta_0.e^{\beta_1 X}+\varepsilon.\] Transformáciou \(\ln \widehat{Y}=\widehat{Z}\), \(\ln b_0=a\), \(b_1=b\) prevádzame bodový odhad \(\widehat{y}=b_0.e^{b_1 X}\) na lineárny model \[\widehat{Z}=a+bX.\]
• mocninová regresia - model, v ktorom je závislosť popísaná mocninovou funkciou \[Y=\beta_0.X^{\beta_1}+\varepsilon\] Transformáciou \(\ln \widehat{Y}=\widehat{Z}\), \(\ln b_0=a\), \(b_1=b\) a \(\ln X=T\) prevádzame bodový odhad \(\widehat{y}=b_0.X^{b_1}\) na lineárny model \[\widehat{Z}=a+bT.\]

Korelačná analýza

Kvalitu (silu, tesnosť) vybranej regresnej funkcie medzi premennými posudzujeme pomocou korelačnej analýzy. Jej úlohou je teda posúdenie tesnosti štatistickej závislosti medzi skúmanými premennými.

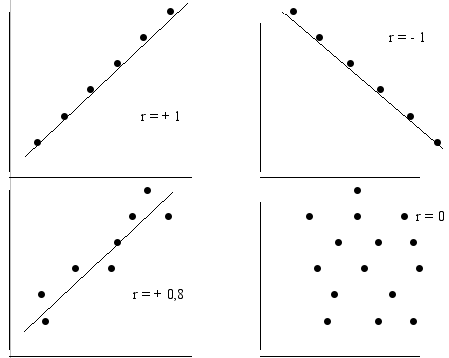
Párový koeficient korelácie (korelačný koeficient) \(\rho_{xy}\) alebo známy aj ako Pearsonov koeficient korelácie meria tesnosť obojstrannej lineárnej závislosti medzi dvoma náhodnými premennými \(X\) a \(Y\) a platí:

• \(\rho_{xy}=0\) - premenné \(X\) a \(Y\) nie sú lineárne závislé;
• \(\rho_{xy}\gt 0\) - medzi premennými \(X\) a \(Y\) je priama lineárna závislosť;
• \(\rho_{xy}\lt 0\) - medzi premennými \(X\) a \(Y\) je nepriama lineárna závislosť.

Koeficient korelácie nadobúda hodnoty z intervalu \(\left<-1;1\right>\) a čím je absolútna hodnota bližšie k hodnote \(1\), tým je lineárna závislosť tesnejšia.  Bodovým odhadom koeficientu korelácie \(\rho_{xy}\) je výberový párový koeficient korelácie \(r_{xy}\), pre ktorý platí: \[r_{xy}=\frac{\overline{xy}-\overline{x}.\overline{y}}{\sqrt{\overline{x^2}-(\overline{x})^2}.\sqrt{\overline{y^2}-(\overline{y})^2}}.\]

Index determinácie \(I^2_{yx}\) meria stupeň závislosti vzhľadom na regresnú funkciu a vypočítame ho podľa vzťahu \[I^2_{yx}=\frac{\sum_{i=1}^n(\widehat{y_i}-\overline{y})^2}{\sum_{i=1}^n(y_i-\overline{y})^2}=1-\frac{\sum_{i=1}^n(y_i-\widehat{y_i})^2}{\sum_{i=1}^n(y_i-\overline{y})^2},\] kde \(y_i\) je nameraná hodnota, \(\widehat{y_i}\) je teoretická hodnota a  \(\overline{y}\) je aritmetický priemer. Nadobúda hodnoty z intervalu \(\left<0;1\right>\) a čím je hodnota bližšie k hodnote \(1\), tým je závislosť silnejšia.

Index korelácie \(I_{yx}\) taktiež meria stupeň závislosti vzhľadom na regresnú funkciu a vypočítame ho podľa vzťahu \[I_{yx}=\sqrt{\frac{\sum_{i=1}^n(\widehat{y_i}-\overline{y})^2}{\sum_{i=1}^n(y_i-\overline{y})^2}}=\sqrt{1-\frac{\sum_{i=1}^n(y_i-\widehat{y_i})^2}{\sum_{i=1}^n(y_i-\overline{y})^2}}.\]

Nadobúda hodnoty z intervalu \(\left<0;1\right>\), no na rozdiel od koeficientu determinácie nie je koeficient korelácie symetrickou mierou závislosti, t.j. \(I_{yx}\neq I_{xy}\).