Exponenciálne rozdelenie

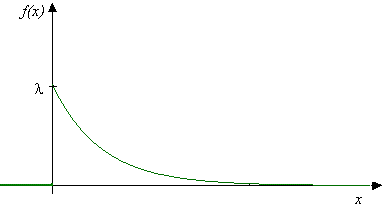
Exponenciálne rozdelenie má pomerne širokú použiteľnosť napr. v teórii spoľahlivosti a životnosti, v teórii hromadnej obsluhy a v teórii obnovy. Dobre popisuje rozdelenie životnosti výrobkov a zariadení, v ktorých sa porucha vyskytne náhodou. Typickými príkladmi náhodnej veličiny s exponenciálnym rozdelením sú  doby čakania na obsluhu alebo doby medzi realizáciou dvoch po sebe nasledujúcich javov.  Spojitá náhodná veličina \(X\) má exponenciálne rozdelenie pravdepodobnosti s parametrom \(\lambda\gt 0\), ak jej hustota pravdepodobnosti \(f(x)\) má tvar: \[f(x)=\begin{cases}{\lambda}e^{-\lambda x},& \hbox{ pre }x\gt 0\\ 0, &\hbox{ pre }x\leq 0\end{cases}\] a stručne zapisujeme \(X\sim Exp(\lambda)\) alebo \(X\sim E(\lambda)\).

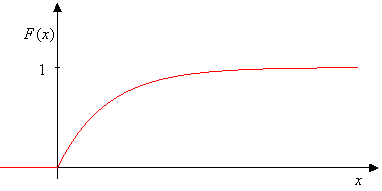
Ak \(X\sim Exp(\lambda)\), tak \[E(X)=\frac{1}{\lambda},\;\;\;\;D(X)=\frac{1}{\lambda^2},\;\;\;\;\sigma(X)=\frac{1}{\lambda},\] \[\widehat{x}=0,\;\;\;\;\tilde{x}=\frac{1}{\lambda}\,\ln 2,\] \[\gamma_1=2,\;\;\;\;\;\gamma_2=9,\] \[F(x)=\begin{cases} 1-e^{-\lambda x},& \hbox{ pre } x\gt 0 \\0,& \hbox{ pre }x\leq 0\end{cases}\]

Exponenciálne rozdelenie je špeciálny prípad Gamma rozdelenia t.j. \(Exp(\lambda)=Gamma(\lambda,1)\) a taktiež špeciálny prípad Weibullovho rozdelenia t.j. \(Exp(\lambda)=W(\lambda,1)\).