Normálne a normované normálne rozdelenie

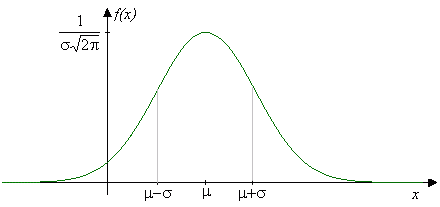
Normálne rozdelenie je najčastejšie používaným rozdelením zo spojitých náhodných premenných. Má podstatný význam v teórii pravdepodobnosti a štatistiky. Používame ho napr. v situáciách, keď na kolísanie náhodnej premennej pôsobí veľký počet  nepatrných, navzájom nezávislých príčin. Za určitých podmienok je ním možné aproximovať aj iné rozdelenia. Spojitá náhodná veličina \(X\) má normálne (Gaussovo) rozdelenie pravdepodobnosti s parametrami \(\mu\), \(\sigma\), kde \(\sigma\gt 0\), ak jej hustota pravdepodobnosti \(f(x)\) má tvar: \[f(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2},\hbox{ pre }x\in\mathbb{R}\] a stručne zapisujeme \(X\sim Norm(\mu,\sigma)\) alebo \(X\sim N(\mu,\sigma^2)\).

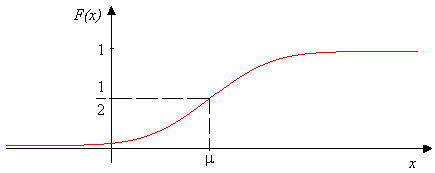
Ak \(X\sim Norm(\mu,\sigma)\), tak \[E(X)=\mu,\;\;D(X)=\sigma^2,\;\;\sigma(X)=\sigma,\] \[\widehat{x}=\mu,\;\;\;\;\tilde{x}=\mu,\] \[\gamma_1=0,\;\;\;\;\;\gamma_2=0,\] \[F(x)=\frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^x e^{-\frac{1}{2}\left(\frac{t-\mu}{\sigma}\right)^2}dt,\hbox{ pre }x\in\mathbb{R}.\]

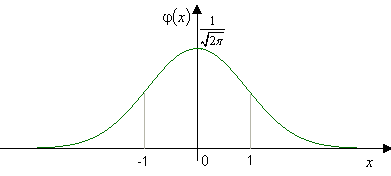
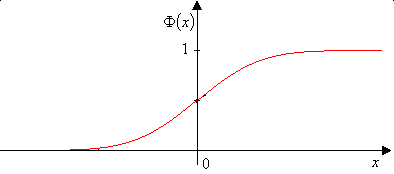
Náhodnú premennú \(Y\) s normálnym rozdelením s parametrami \(\mu=0\) a \(\sigma=1\) nazývame normovanou normálnou náhodnou premennou a zapisujeme \(Y\sim Norm(0,1)\) alebo \(Y\sim N(0,1)\). Jej hustota pravdepodobnosti má tvar \[\varphi(y)=\frac{1}{\sqrt{2\pi}}e^{-\frac{y^2}{2}},\hbox{ pre }y\in\mathbb{R}\] a distribučná funkcia  \[\varPhi(y)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^ye^{-\frac{t^2}{2}}dt,\hbox{ pre }y\in\mathbb{R}.\]

Ak \(X\sim Norm(\mu,\sigma)\), tak pomocou lineárnej transformácie \(Y=\frac{X-\mu}{\sigma}\) dostávame náhodnú premennú  \(Y\), pre ktorú  platí: \(Y\sim Norm(0,1)\). Takejto vlastnosti hovoríme normalizácia alebo normovanie náhodnej premennej \(X\). Pre stanovenie hodnôt distribučnej funkcie \(\varPhi(y)\) je potrebné použiť matematický softwér alebo štatistické tabuľky pre nezáporné hodnoty. V niektorých prípadoch je užitočné použiť  vlastnosť hustoty \(\varphi(y)\) a distribučnej funkcie \(\varPhi(y)\):

1. Funkcia \(\varphi(y)\) je párna, t.j. \(\varphi(y)=\varphi(-y)\),
2. \(\varPhi(-y)=1-\varPhi(y)\),
3. \(\varPhi(y)-\varPhi(-y)=2\varPhi(y)-1\).