Rovnomerné rozdelenie

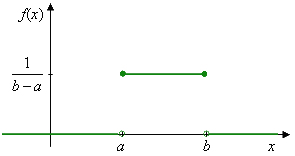
Rovnomerným rozdelením sa riadia náhodné premenné, ktoré majú rovnakú možnosť nadobudnúť ktorúkoľvek  hodnotu  z nejakého konečného intervalu. Napr. chyby pri zaokrúhľovaní čísel, doby čakania na uskutočnenie javu opakujúceho sa v pravidelných časových intervaloch. Spojitá náhodná veličina \(X\) má rovnomerné rozdelenie pravdepodobnosti s parametrami \(a\), \(b\), resp. na intervale \(\left<a,b\right>\),  ak jej hustota pravdepodobnosti \(f(x)\) má tvar: \[f(x)=\begin{cases}\frac{1}{b-a},& \hbox{ pre }x\in\left<a,b\right>\\ 0, &\hbox{ pre }x\notin\left<a,b\right>\end{cases}\] a stručne zapisujeme \(X\sim Unif(a,b)\) alebo \(X\sim R(a,b)\).

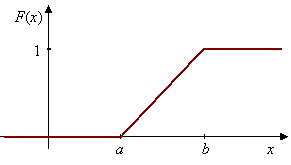
Ak \(X\sim Unif(a,b)\), tak \[E(X)=\frac{a+b}{2},\;\;D(X)=\frac{(b-a)^2}{12},\;\;\sigma(X)=\frac{(b-a)}{2.\sqrt{3}},\] \[\nu=\frac{1}{\sqrt{3}}\frac{b-a}{a+b},\;\;\;\;\tilde{x}=\frac{a+b}{2},\] \[\gamma_1=0,\;\;\;\;\;\gamma_2=\frac{9}{5},\] \[F(x)=\begin{cases}0,& \hbox{ pre }x\leq a\\ \frac{x-a}{b-a},& \hbox{ pre }x\in\left( a,b\right>\\1, &\hbox{ pre }b\lt x.\end{cases}\]