Popisná štatistika
Štatistické spracovanie údajov
Pod štatistickým znakom rozumieme vonkajší postihnuteľný, merateľný prejav skúmanej premenlivej vlastnosti štatistických jednotiek. Podľa spôsobu vyjadrenia ich všeobecne delíme na
- kvalitatívne - vyjadrujú číselné alebo merateľné vlastnosti štatistických jednotiek číslami a delíme ich na spojité a diskrétne. Spojité nadobúdajú ľubovoľné hodnoty z ohraničeného alebo neohraničeného intervalu. Diskrétne nadobúdajú izolované číselné hodnoty.
- kvantitatívne - slovne popisujú vlastnosti štatistických jednotiek. Podľa toho koľko variantov môže nadobúdať slovný znak ich delíme na množné a alternatívne.
Prvým krokom pri spracovaní údajov štatistického súboru je ich utriedenie. Poznáme dve základné triedenia údajov, a to triedenie do variačného radu a triedenie do intervalov.
Triedenie do variačného radu - hodnoty štatistického znaku usporiadame podľa veľkosti vzostupnom poradí, t.j. od najnižšej hodnoty po najvyššiu, pričom rovnaké hodnoty zapíšeme toľkokrát, koľkokrát sa vyskytujú. xj označuje hodnotu štatistického znaku na j-tej pozícii vo vytvorenom variačnom rade, ktorý môžeme následne zapísať v tvare 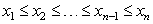 . Nech k je celkový počet rôznych hodnôt znaku, niekedy sa pre dané k používa pojem počet tried. Pre
. Nech k je celkový počet rôznych hodnôt znaku, niekedy sa pre dané k používa pojem počet tried. Pre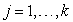 počet štatistických jednotiek s rovnakou hodnotou xj nazývame absolútnou početnosťou hodnoty xj a označujeme ju nj. Pomocou absolútnej početnosti nj definujeme absolútnu kumulatívnu početnosť vzťahom
počet štatistických jednotiek s rovnakou hodnotou xj nazývame absolútnou početnosťou hodnoty xj a označujeme ju nj. Pomocou absolútnej početnosti nj definujeme absolútnu kumulatívnu početnosť vzťahom 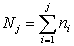 a relatívnu početnosť vzťahom
a relatívnu početnosť vzťahom 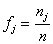 . Pomocou relatívnych početností môžeme definovať relatívnu kumulatívnu početnosť
. Pomocou relatívnych početností môžeme definovať relatívnu kumulatívnu početnosť 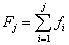 . Pre štatistický súbor s k rôznymi hodnotami potom platí
. Pre štatistický súbor s k rôznymi hodnotami potom platí 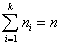 a
a 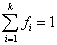 .
.
Triedenie do intervalov - v štatistických súboroch s rozsahom aspoň 50 znakov, ale aj v menších súboroch, triedime štatistický súbor do skupín, resp. intervalov. V prvom kroku je potrebné stanoviť počet tried a to tak, aby počet tried nebol príliš malý čím by sa stratila podstatná časť informácie, no nesmie byť ani príliš veľký čím by sa znížila prehľadnosť a zároveň zvýšila aj výpočtová zložitosť. Poznáme mnoho kritérií na určenie vhodného počtu k tried a tak uvádzame aspoň niekoľko z nich
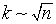
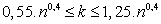
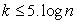
![]()
Pri triedení štatistických jednotiek do tried musíme dodržať dve zásady, a to: zásada úplnosti - triedy musia byť vytvorené tak, aby každá jednotka mohla byť zatriedená do niektorej z tried; zásada jednoznačnosti - triedy musia byť vytvorené tak, aby o každej jednotke bolo jednoznačne rozhodnuté, do ktorej z tried má byť zaradená. Pre každé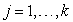 definujeme j-tý triedny interval v tvare
definujeme j-tý triedny interval v tvare 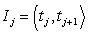 alebo
alebo 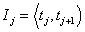 , kde tj je dolná hranica a tj+1 je horná hranica. Reprezentantom intervalu Ij je aritmetický priemer jeho koncových hraníc. Využitím variačného rozpätia
, kde tj je dolná hranica a tj+1 je horná hranica. Reprezentantom intervalu Ij je aritmetický priemer jeho koncových hraníc. Využitím variačného rozpätia  stanovíme dĺžku triedneho intervalu h podľa vzťahu
stanovíme dĺžku triedneho intervalu h podľa vzťahu 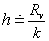 , kde zaokrúhľujeme smerom nahor.
, kde zaokrúhľujeme smerom nahor.
Grafické zobrazenie štatistického súbor - grafy sú ďalším dôležitým vyjadrovacím prostriedkom štatistiky, nakoľko grafické zobrazovanie nám môže poslúžiť pre rýchlu a hlavne názornú prezentáciu štatistických výsledkov. Pri grafickom znázornení sa používa súradnicová pravouhlá sústava, kde na x-ovú os nanášame hodnoty znaku, resp. triedne intervaly alebo ich stredy a na y-ovú os príslušné početnosti. Poznáme niekoľko typov diagramov, a to:
- bodové diagramy - grafy, v ktorých na y-ovú os môžeme naniesť absolútne, absolútne kumulatívne, relatívne alebo relatívne kumulatívne početnosti.
- spojnicové diagramy - bodové diagramy, v ktorých sú jednotlivé body spojené lomenou čiarou. Špeciálnym typom je polygón.
- histogram - stĺpcový graf, v ktorom nad úsekom na x-ovej osi rovným dĺžke triedneho intervalu nakreslíme obdĺžnik, ktorého výška je určená absolútnou početnosťou.
- kruhové, koláčové grafy - kruh rozdelený na výseky.
Číselné charakteristiky
Štatistické spracovanie nazbieraných údajov vo forme rozdelenia početností, tabuľky alebo grafu poskytujú len základné informácie o štatistickom súbore nakoľko takéto roztriedenie je len akýmsi podkladom pre popis a vzájomné porovnanie viacerých súborov. Ak chceme docieliť jednoznačné vzájomné porovnávanie dvoch alebo niekoľkých štatistických súborov, tak potrebujeme vhodné veličiny, ktoré budú číselne charakterizovať základné vlastnosti rozdelenia početnosti. Takéto veličiny sa nazývajú číselné charakteristiky a najznámejšími sú tieto tri kategórie číselných charakteristík:
- charakteristiky polohy - predstavujú určitú úroveň resp. polohu znaku, okolo ktorého sú zvyšné hodnoty štatistického súboru koncentrované. Túto polohu meriame pomocou rôznych druhov stredných hodnôt ako: aritmetický, harmonický a geometrický priemer, modus, medián a kvantily.
- charakteristiky variability - vyjadrujú odlišnosti (variabilitu, rozptyl) hodnôt štatistického súboru a sú dôležitým faktorom v prípade porovnania súborov, v ktorých sú charakteristiky polôh totožné. Najznámejšími sú: kvantilové, kvartilové a variačné rozpätie, kvartilová odchýlka, priemerná odchýlka, pomerná priemerná odchýlka, rozptyl, smerodajná odchýlka a variačný koeficient.
- charakteristiky miery šikmosti a špicatosti - pre ich výpočet sú potrebné momentové charakteristiky. Najznámejšími sú: koeficient šikmosti, koeficient špicatosti a Pearsonova miera šikmosti.
Pri výpočte zmienených charakteristík používame dva typy vzorcov. Ak sú údaje štatistického súboru neutriedené, tak použijeme jednoduchý vzorec (uvedený bude na prvom mieste). Ak sú údaje štatistického súboru usporiadané do variačného radu rozdelenia alebo do intervalového rozdelenia, tak použijeme vážený vzorec (uvedený bude na druhom mieste, kde k je počet tried, resp. intervalov).
Aritmetický priemer -
![]()
![]()
Harmonický priemer -
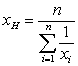
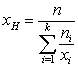
Geometrický priemer -
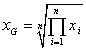
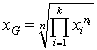
Pre vyššie uvedené priemery všeobecne platí ![]() a rovnosť nastáva len v prípade, ak sú všetky hodnoty znakov v súbore rovnaké.
a rovnosť nastáva len v prípade, ak sú všetky hodnoty znakov v súbore rovnaké.
Modus - predstavuje najpočetnejšiu hodnotu štatistického súboru a označujeme ho Mo alebo ![]() . V prípade radu rozdelenia početností zodpovedá modus hodnote znaku s najväčšou absolútnou početnosťou. Ak je daná hodnota jediná, tak rozdelenie je unimodálne, v opačnom prípade je polymodálne. V prípade intervalového rozdelenia početností určíme modus podľa nasledovného vzťahu
. V prípade radu rozdelenia početností zodpovedá modus hodnote znaku s najväčšou absolútnou početnosťou. Ak je daná hodnota jediná, tak rozdelenie je unimodálne, v opačnom prípade je polymodálne. V prípade intervalového rozdelenia početností určíme modus podľa nasledovného vzťahu
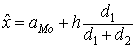
kde aMo je začiatok modálneho intervalu; h je dĺžka intervalu; d1 je rozdiel medzi absolútnou početnosťou modálneho a predchádzajúceho intervalu; d2 je rozdiel medzi absolútnou početnosťou modálneho a nasledujúceho intervalu. Modálnym intervalom chápeme interval, v ktorom sa nachádza hľadaný modus.
Medián - predstavuje prostrednú hodnotu štatistického súboru, v ktorom sú hodnoty usporiadané do neklesajúcej postupnosti. Označujeme ho Me alebo ![]() . Ak n je rozsah štatistického súboru a xi je znak na i-tej pozícii, tak
. Ak n je rozsah štatistického súboru a xi je znak na i-tej pozícii, tak
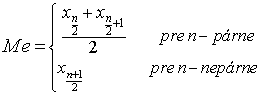
V prípade intervalového rozdelenia početnosti medián vypočítame podľa vzťahu
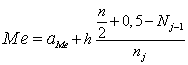
kde aMe je začiatok mediánového intervalu; h je dĺžka intervalu; Nj-1 je absolútna kumulatívna početnosť intervalu pred mediánovým; nj je absolútna početnosťou mediánového intervalu. Mediánovým intervalom chápeme interval, v ktorom sa nachádza medián.
Rozlišujeme tri prípady v závislosti od toho, aká je vzájomná poloha modusu, mediánu a aritmetického priemeru skúmaného štatistického súboru. Ak 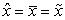 , tak hovoríme o symetrickom rozdelení početnosti. Ak
, tak hovoríme o symetrickom rozdelení početnosti. Ak 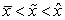 , tak hovoríme o zápornom zošikmení. V prípade
, tak hovoríme o zápornom zošikmení. V prípade 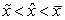 hovoríme o kladnom zošikmení.
hovoríme o kladnom zošikmení.
Kvantily - číselné hodnoty, ktoré rozdeľujú utriedené hodnoty štatistického súboru v neklesajúcom poradí na k rovnako početných častí. Najznámejšími sú: medián (pre k=2), kvartily (pre k=4), decily (pre k=10) a percentily (pre k=100).
Dolný kvartil - pre intervalové rozdelenie početnosti platí
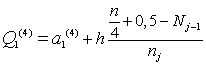
kde a1(4) je začiatok dolného kvartilového intervalu; h je dĺžka intervalu; Nj-1 je absolútna kumulatívna početnosť intervalu pred dolným kvartilovým intervalom; nj je absolútna početnosťou dolného kvartilového intervalu. Dolným kvartilovým intervalom chápeme interval, v ktorom sa nachádza dolný kvartil.
Horný kvartil - pre intervalové rozdelenie početnosti platí
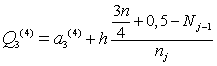
kde a3(4) je začiatok horného kvartilového intervalu; h je dĺžka intervalu; Nj-1 je absolútna kumulatívna početnosť intervalu pred horným kvartilovým intervalom; nj je absolútna početnosťou horného kvartilového intervalu. Horným kvartilovým intervalom chápeme interval, v ktorom sa nachádza horný kvartil.
Kvantilové rozpätie - počítame podľa vzťahu 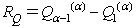 , kde
, kde 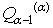 je horný kvantil a
je horný kvantil a 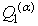 je dolný kvantil.
je dolný kvantil.
Kvartilové rozpätie - počítame podľa vzťahu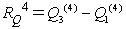 , kde Q3(4) je horný kvartil a Q1(4) je dolný kvartil.
, kde Q3(4) je horný kvartil a Q1(4) je dolný kvartil.
Variačné rozpätie - počítame podľa vzťahu ![]() , kde xmax je maximálna hodnota a xmin je minimálna hodnota.
, kde xmax je maximálna hodnota a xmin je minimálna hodnota.
Kvartilová odchýlka - počítame podľa vzťahu 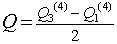 , kde Q3(4) je horný kvartil a Q1(4) je dolný kvartil.
, kde Q3(4) je horný kvartil a Q1(4) je dolný kvartil.
Priemerná odchýlka - určuje o koľko sa navzájom odlišujú zistené hodnoty v štatistickom súbore v priemere od ich aritmetického priemeru.
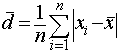
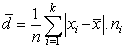
Pomerná priemerná odchýlka - počítame podľa vzťahu ![]()
Rozptyl - je jednou z najpoužívanejších charakteristík variability a označujeme ho s2. Zodpovedá aritmetickému priemeru štvorcov odchýliek hodnôt štatistického znaku od ich aritmetického priemeru.
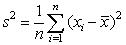
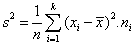
Smerodajná odchýlka - je definovaná ako kladná odmocnina z rozptylu a označujeme ju s. Čim väčšia je odlišnosť hodnôt štatistického súboru, tým väčšia je aj hodnota smerodajnej odchýlky. Výpočtový vzorec je 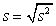 .
.
Variačný koeficient - udávame v percentách a počítame podľa vzťahu 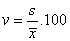 .
.
Všeobecný moment r-tého rádu - označujeme ho 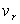 a definujeme pre prirodzené číslo r v tvare
a definujeme pre prirodzené číslo r v tvare
![]()
![]()
Centrálny moment r-tého rádu - označujeme ho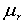 a definujeme pre prirodzené číslo r v tvare
a definujeme pre prirodzené číslo r v tvare
![]()
![]()
Koeficient šikmosti - známy je aj ako koeficient asymetrie a definujeme ho pomocou centrálneho momentu tretieho rádu a smerodajnej odchýlky vzťahom 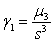 . Popisuje rozloženie hodnôt štatistického súboru vzhľadom na polohu aritmetického priemeru. Ak
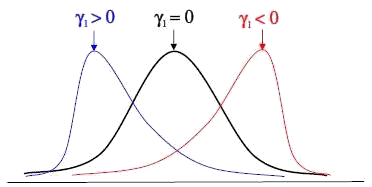
. Popisuje rozloženie hodnôt štatistického súboru vzhľadom na polohu aritmetického priemeru. Ak 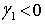 , tak väčšina hodnôt leží naľavo od aritmetického priemeru (ľavostranná asymetria). Ak
, tak väčšina hodnôt leží naľavo od aritmetického priemeru (ľavostranná asymetria). Ak 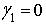 , tak hodnoty sú symetricky rozložené okolo aritmetického priemeru. Ak
, tak hodnoty sú symetricky rozložené okolo aritmetického priemeru. Ak 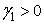 , tak väčšina hodnôt leží napravo od aritmetického priemeru (pravostranná asymetria). Inak povedané, znamienko daného koeficientu určuje smer asymetrie a hodnota koeficientu určuje silu asymetrie.
, tak väčšina hodnôt leží napravo od aritmetického priemeru (pravostranná asymetria). Inak povedané, znamienko daného koeficientu určuje smer asymetrie a hodnota koeficientu určuje silu asymetrie.
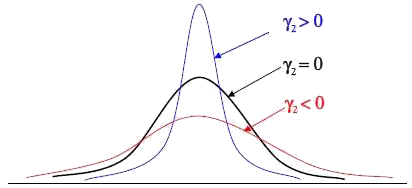
Koeficient špicatosti - známy je aj ako koeficient excesu a definujeme ho pomocou centrálneho momentu štvrtého rádu a smerodajnej odchýlky vzťahom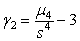 . Meria stupeň koncentrácie hodnôt štatistického znaku okolo strednej hodnoty. Ak
. Meria stupeň koncentrácie hodnôt štatistického znaku okolo strednej hodnoty. Ak 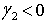 , tak polygón relatívnych početností je plochejší ako krivka normálneho rozdelenia. Ak
, tak polygón relatívnych početností je plochejší ako krivka normálneho rozdelenia. Ak 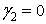 , tak polygón relatívnych početností má rovnakú špicatosť ako krivka normálneho rozdelenia. Ak
, tak polygón relatívnych početností má rovnakú špicatosť ako krivka normálneho rozdelenia. Ak 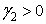 , tak polygón relatívnych početností je špicatejší ako krivka normálneho rozdelenia. Špicatosť je tým väčšia, čím viac sa koeficient líši od nuly.
, tak polygón relatívnych početností je špicatejší ako krivka normálneho rozdelenia. Špicatosť je tým väčšia, čím viac sa koeficient líši od nuly.
Pearsonova miera šikmosti - počítame podľa vzťahu 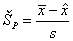 a platia preň rovnaké vlastnosti ako pre koeficient šikmosti.
a platia preň rovnaké vlastnosti ako pre koeficient šikmosti.
Páči sa Vám tento web venovaný matematike?
