Náhodná veličina (premenná)

Pojem náhodnej veličiny

V pravdepodobnostnej teórii sa jednotlivým javom priraďovali číselné hodnoty a  výsledkom pokusu bolo nejaké číslo, ktorého hodnota bola jednoznačne určená elementárnym javom. Priradenie však nemusí byť jednoznačné, a tak rôznym elementárnym javom môže byť priradené to isté číslo. Podobne by to mohlo byť aj v prípade náhodných pokusov, ktorých výsledok má kvalitatívny charakter. Napr.: Ak je pozitívny výsledok, priradíme číslo $1$. V prípade negatívneho výsledku, priradíme číslo $0$. Pôvodné náhodné javy nahradíme určitými hodnotami $x$ nejakej premennej veličiny $X$, ktorú nazývame náhodnou veličinou (premenou). Podľa dohody sa náhodné veličiny označujú veľkými písmenami $X$, $Y$, $Z$ a hodnoty náhodných premenných malými písmenami $x,\, y,\, z$. V rôznych aplikáciách sa stretávame s náhodnými veličinami dvojakého typu:

1. Diskrétna náhodná veličina - môže nadobúdať len hodnoty  z konečnej alebo spočítateľnej množiny. Napr.: počet študentov 1. ročníka na fakulte; počet dievčat medzi žiakmi v triede; počet chybných nepodarkov medzi $n$ náhodne vybranými výrobkami zo sady; počet zákazníkov, ktorí prídu do predajne za daný čas.
2. Spojitá náhodná veličina - môže nadobúdať všetky hodnoty z konečného alebo nekonečného intervalu reálnych čísel. Napr.: životnosť stroja; doba čakania zákazníka na obsluhu; doba bezporuchového chodu zariadenia; čas potrebný na vykonanie výrobnej operácie.

Rozdelenie náhodnej veličiny

Každá náhodná veličina je jednoznačne určená svojimi pravdepodobnostnými zákonitosťami, a tak  je potrebné stanoviť číselné hodnoty,  ktoré môže daná náhodná veličina nadobúdať a taktiež s akou pravdepodobnosťou ich nadobúda. Takéto pravidlo pre náhodnú veličinu, ktoré každej hodnote, resp. množine hodnôt z intervalu priradí konkrétnu pravdepodobnosť, nazývame rozdelenie náhodnej veličiny. Pravdepodobnostné správanie sa  náhodnej veličiny $X$  môže byť popísané napr. distribučnou funkciou, označenie $F$, ktorá každému reálnemu číslu $x$ priraďuje pravdepodobnosť toho, že náhodná veličina $X$ nadobudne hodnoty menšie ako toto číslo $x$.  Pre každé reálne číslo $x$ je určená predpisom: $F(x)=P(X\lt x )$.

1. Rozdelenie diskrétneho typu - náhodná veličina $X$ sa nazýva diskrétna, ak hodnoty $x_1,\dots,x_n$ nadobúda s pravdepodobnosťami $p_1,\dots,p_n$ a platí: $$p_i=P(X=x_i) \;\;\;\;\;\;\;\sum_{i=1}^{n\,(\infty)}p_i=1.$$ Pre distribučnú funkciu $F(x)$ náhodnej veličiny $X$ platí: $\displaystyle F(x)=\sum_{x_i\lt x}p_i$.
2. Rozdelenie spojitého typu - náhodná veličina $X$ sa nazýva spojitá, ak existuje reálna, nezáporná funkcia $f(x)$ a pre distribučnú funkciu $F(x)$ náhodnej veličiny $X$ platí: $\displaystyle F(x)=\int_{-\infty}^xf(t)\,dt$ pre každé reálne číslo $x$. Funkcia $f(x)$ sa nazýva hustota pravdepodobnosti a platí: $$f(x)\geq 0\;\;\;\;\;\;\;\;\; \int_{-\infty}^{\infty}f(x)\,dx=1.$$

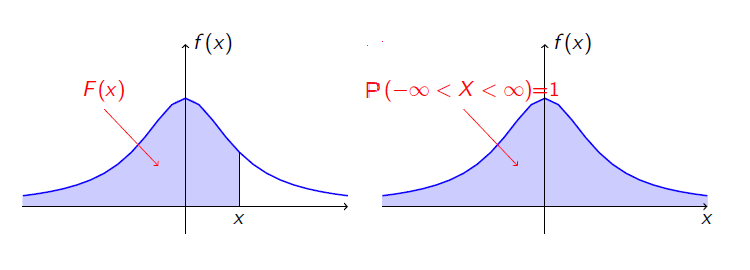
Nasledovný obrázok bližšie interpretuje geometrický význam distribučnej funkcie, hustoty a pravdepodobnosti náhodnej veličiny.

Vlastnosti distribučnej funkcie $F(x)$ náhodnej veličiny $X$:

• pre každé  $x\in \mathbb{R}$ platí: $0\leq F(x)\leq 1$,
•  $\displaystyle \lim_{x\to-\infty}F(x)=0$  a $\displaystyle \lim_{x\to\infty}F(x)=1$ ,
• pre každé dve čísla $a,\, b$ také, že: $a \lt b$ platí: $P(a\leq x\lt b)=F(b)-F(a)$,
• funkcia $F(x)$ je neklesajúca,
• funkcia $F(x)$ je spojitá zľava a ak $X$ je spojitá náhodná veličina, tak $F(x)$ spojitá.
• Pre spojitú náhodnú veličinu $X$ a pre každé  $x\in \mathbb{R}$ platí: $f^{'}(x)=F(x)$.

Číselné charakteristiky náhodnej veličiny

Dôležité informácie o náhodnej veličine môžu byť charakterizované aj pomocou jedného alebo viacerých čísel, ktoré nazývame číselnými charakteristikami náhodnej veličiny. Najznámejšími sú práve dve kategórie číselných charakteristík:

1. charakteristiky polohy - udávajú polohu daného rozdelenia a reprezentujú akýsi stred celého rozdelenia, okolo ktorého sa budú vyskytovať hodnoty náhodnej veličiny pri opakovaných pokusoch. Medzi takéto charakteristiky patria: stredná hodnota, medián a modus.

2. charakteristiky variability - určujú, či sa rozdelenia náhodných veličín odlišujú v rozsahu, kolísaní hodnôt, koncentráciou alebo rozptýlením (variabilitou). Medzi takéto charakteristiky patria: disperzia  (rozptyl) a smerodajná odchýlka.

Na nasledovnom obrázku  sú znázornené hustoty rôznych náhodných veličín. Náhodné veličiny s rovnakými strednými hodnotami a rôznymi disperziami, resp. s rôznymi strednými hodnotami a rovnakými disperziami.

Stredná hodnota náhodnej veličiny $X$ - ak existuje, tak je to číslo $E(X)$ definované vzťahom: 

• $\displaystyle E(X)=\sum_{i=1}^{n\;(\infty)}x_i.p_i$ - pre diskrétnu náhodnú veličinu $X$
• $\displaystyle E(X)=\int_{-\infty}^{\infty}x.f(x)dx$ - pre spojitú náhodnú veličinu $X$

Vlastnosti strednej hodnoty:

Nech $X$ je náhodná veličina a nech $a,\, b$ sú konštanty. Potom:

• $E(a)=a$,
• $E(aX+b)=aE(X)+b$,
• $E\left(X-E(X)\right)=0$.

Modus náhodnej veličiny $X$ - označujeme $M_o(X)$ Pre diskrétnu náhodnú veličinu je definovaný ako najpravdepodobnejšia hodnota náhodnej veličiny; pre spojitú náhodnú veličinu ako ľubovoľný bod, v ktorom jej hustota nadobúda lokálne maximum.

Disperzia (rozptyl) náhodnej veličiny $X$ - ak existuje, tak je to číslo $D(X)$ a je definované ako stredná hodnota náhodnej veličiny $\left( X-E(X)\right)^2$ t.j. $\displaystyle D(X)=E\left[\left( X-E(X)\right)^2\right]$. V závislosti od typu náhodnej veličiny $X$ definujeme $D(X)$ vzťahom:

•  $\displaystyle D(X)=\sum_{i=1}^{n\;(\infty)}(x_i-E(X))^2.p_i$ - pre diskrétnu náhodnú veličinu $X$
•  $\displaystyle D(X)=\int_{-\infty}^{\infty}(x-E(X))^2.f(x)dx$ - pre spojitú náhodnú veličinu $X$

Vlastnosti disperzie:

Nech $X$ je náhodná veličina a nech $a,\, b$ sú konštanty. Potom:

• $D(a)=0$,
• $D(aX+b)=a^2.D(X)$,
• $D(X)=E(X^2)-\left(E(X)\right)^2$ - na výpočet disperzie sa používa tento výpočtový vzťah.

Ak existuje disperzia $D(X)$ náhodnej veličiny $X$, tak smerodajná odchýlka náhodnej veličiny $X$ je  číslo $\sigma(X)$ definované predpisom $\sigma(X)=\sqrt{D(X)}$.

Kvantilová funkcia  náhodnej veličiny $X$ - je funkcia $F^{-1}$ definovaná vzťahom $F^{-1}(p)=\inf\{x; F(x)\geq p\}$  pre $0\lt p\lt 1$. Hodnoty $F^{-1}(p)$ sa nazývajú 100.p % - né kvantily a označujeme ich $x_p$.

Medián náhodnej veličiny $X$ - kvantilová charakteristika Me$(X)$, ktorá zodpovedá $50$%-nému kvantilu. Inak povedané, medián je hodnota, ktorá interval možných hodnôt náhodnej veličiny rozdelí na dva rovnako pravdepodobné intervaly.